

Un modèle simple et global de mortalité
Nous proposons ici un modèle global de la mortalité permettant une bonne estimation des quotients annuels. Il se réduit à :
 Le
sous-modèle des « vieux »
Le
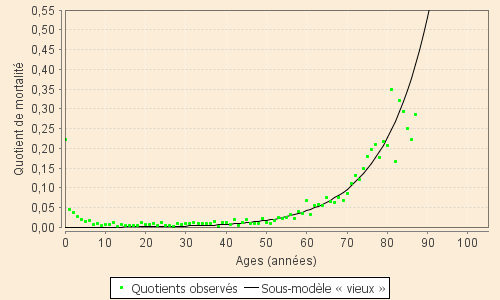
sous-modèle des « vieux »Nous utilisons le modèle exponentiel de Gompertz en tenant compte de l'aménagement nécessaire au XVIIe siècle et en l'extrapolant aux âges les plus faibles pour lesquels le modèle donne des probabilités de décès infimes comme le montre le graphique ci-contre se rapportant à la période XVIII-2. Le modèle de Gompertz est parfaitement susceptible de s'adapter au fait qu'il n'y a pas d'âge minimal précis pour pouvoir mourir de « vieillesse » et au fait que l'âge auquel débuterait la mortalité des « vieux » est très variable au cours des siècles comme l'expérience des archives le montrent.
Le modèle comporte deux paramètres.
Ce sous-modèle est plus difficile à établir que celui des « vieux ». En effet, si l’on connaît son début (l’âge 0), on ne sait pas quand il doit prendre fin. On ne connaît donc pas la forme qu’il doit prendre.
Nous tentons d’aborder ce dernier point de la façon suivante :
La différence traduit alors le nombre des décès qui ne seraient pas dus à la « vieillesse » et nous observons l’évolution de leur nombre en fonction de l’âge au décès.
Le graphique suivant montre ces résultats sous forme de la proportion des morts cumulés avant un âge donné parmi les naissances d’une génération en prenant l’exemple des natifs de la période XVIII-2 (1751 - 1800) représentant un stade moyen sur toute l’entendue temporelle de notre étude (décès totaux en rouge, décès de type « vieux » en bleu et autres décès en noir).
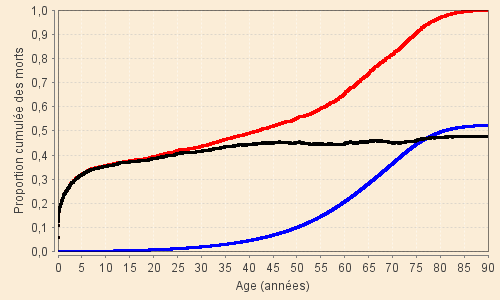
La courbe de mortalité de ceux qui ne meurent pas de « vieillesse » (courbe noire) représente :
L'expérience des archives montre que des personnes meurent suivant un régime « jeune » bien après 5 ans.
Ces faits conduisent logiquement à une poursuite progressivement décroissante de la mortalité de type « jeune » bien au-delà des toutes premières années.
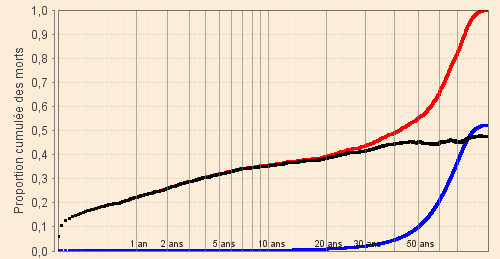
Pour mieux analyser les âges de 0 à 40 ans, nous utilisons la transformation du temps proposé par Bourgeois Pichat qui dilate l’échelle des âges faibles et réduit celle des âges plus élevés comme le présente le graphique ci-contre.
Au plan historique, la réalisation de tels graphiques concernant les natifs de nos trois siècles d'étude permet de constater qu'à sa fin de vie un Fontcouvertin a à peine plus de chance de mourir suivant le modèle « vieux » que suivant le modèle « jeunes ». Plus exactement, le rapport des valeurs finales de ces deux modèles décroît assez régulièrement mais très faiblement de 0,89 pour la génération 1601 - 1650 à 0,67 pour la génération 1876 - 1925, ce qui traduit l'allongement de la durée de vie. Cependant, une exception très significative se fait remarquer, une fois de plus, pour le début du XVIIIe siècle où les générations 1701 - 1750 et 1726 - 1775 atteignent respectivement 2,02 et 1,50 du fait de l'accroissement brutal de la mortalité des jeunes enfants.
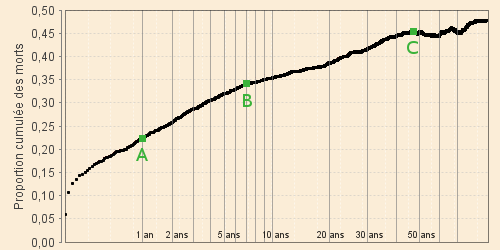
La courbe noire peut alors être approximée par deux segments de droite de 1 an à 7 ans et de 7 ans à 48 ans suivis d'un troisième horizontal traduisant la stabilisation du cumul des décès à partir de 48 ans. Ces limites définies à vue sont représentées par les points verts A, B et C du graphique ci-contre.
Pour définir objectivement ces droites nous déterminons leur pente par régression par moindres carrés sur les valeurs de chaque segment. Cette objectivité conduit à ce que les intersections retenues aux points B et C ne sont pas rigoureusement sur les limites fixées. Par ailleurs, la différence des pentes observée de part et d'autre des points A, B et C conduit à une discontinuité des valeurs calculables des coefficients annuels de mortalité ; cet effet est mineur dans l'absolu puisqu'il porte sur des valeurs très faibles des coefficients. L'erreur relative n'est cependant pas négligeable (voir par exemple les discontinuités des modèles vers 5 ans). Ce problème peut être facilement réglé en augmentant, si nécessaire, le nombre de segments d'ajustement de la courbe de Bourgeois Pichat.
Un calcul des quotients de mortalité annuelle peut s'ensuivre.
Soient N le nombre de naissances de la génération et ja la proportion des individus de la génération n'ayant pas atteint exactement l'âge révolu a + 1.
Le nombre de survivants à l'âge révolu a est N * (1 - ja) et le nombre de mourants dans l'année d'âge révolu a est N * (ja+1 - ja). Le quotient de mortalité à l'âge a est alors qa = (ja+1 - ja) / (1 - ja).
Le quotient de mortalité à 0 an (q0), qui inclut la très forte mortalité initiale, se calcule avec j0 = 0.
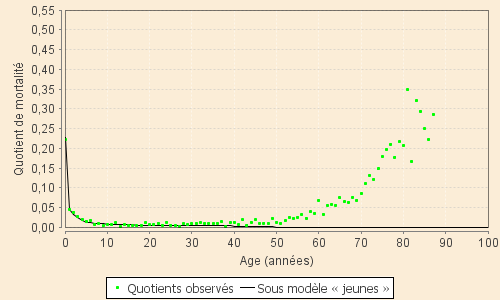
Le graphique ci-contre est relatif à la période XVIII-2 et donne les variations du coefficient annuel de mortalité entre 0 et 100 ans telles que données par le modèle. Il suit correctement la mortalité observée, malgré ses variations très fortes et rapides, jusque vers 25 ans. Il devient extrêmement faible jusqu'à 40 ans et prend des valeurs strictement nulles dès 50 ans.
Les quotients de mortalité issus du sous-modèle des « jeunes » sont ainsi estimés, avec une bonne approximation, par :
soit 5 paramètres à ajuster pour chaque génération étudiée.
La période d'âges plus ou moins longue pendant laquelle la mortalité reste très faible aux âges intermédiaires est alors, dans notre modèle, celle pendant laquelle se superposent la mortalité très faible et décroissante avec l'âge du modèle des « jeunes » et celle encore extrêmement faible mais croissante du modèle des « vieux ».
Le modèle s'adapte bien au XVIIe siècle, époque au cours de laquelle l'épisode des âges intermédiaire est particulièrement courte (10 - 20 ans).
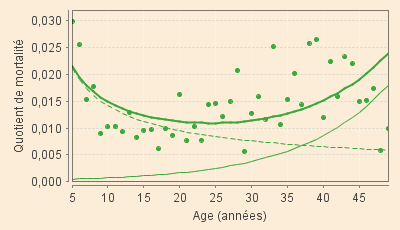
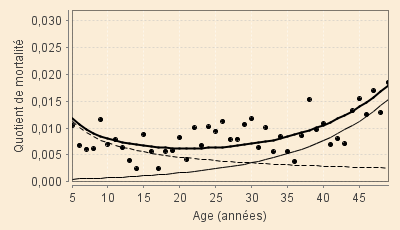
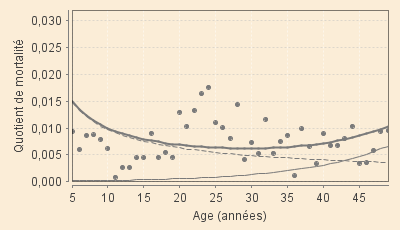
Aux XVIIIe et XIXe siècles, les graphiques suivants, superposant aux quotients annuels observés les valeurs données par les deux sous-modèle (modèle « jeunes » en tireté, modèle « vieux » en trait plein fin, ainsi que leur somme en trait plein fort), traduisent bien l'allongement de cet épisode au cours du temps. On doit noter que les valeurs des coefficients sont extrèmement faibles (de l'ordre de 0,01 au XVIIIe siècle et 0,006 au XIXe) ce qui explique la très grande dispersion graphique des quotients observés (à titre d'exemple, les valeurs relativement élevées observées dans la deuxième moitié du XIXe siècle aux âges voisins de 25 ans sont pour leur plus grande partie dues aux décès de soldats pendant la Grande Guerre... évènements difficilement modélisable à l'état-major du maréchal Foch !)
| XVIII-1 (1701 - 1750) | XVIII-2 (1751 - 1800) |
 |
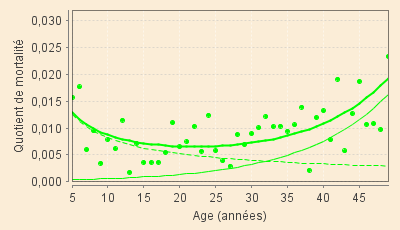 |
| XIX-1 (1801 - 1850) | XIX-2 (1851 - 1900) |
 |
 |
On constate que le calage du modèle des « vieux » à des âges croissant avec les siècles ajuste bien la longueur de la période d'âges intermédiaires pendant laquelle les quotients sont très faibles.
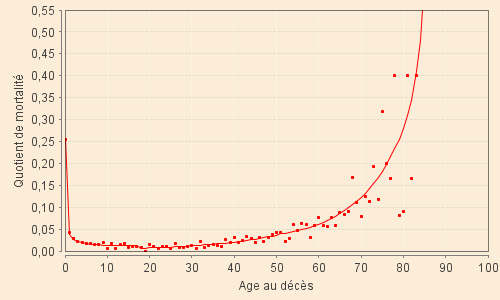
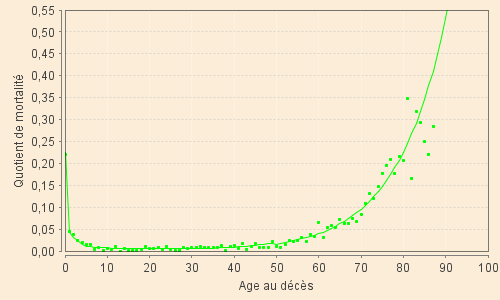
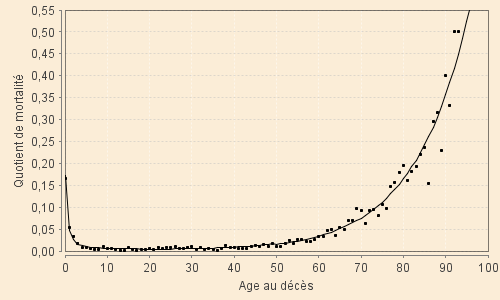
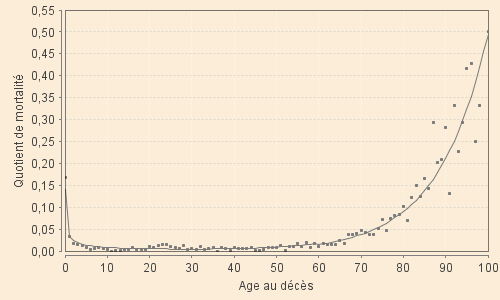
Enfin, voici les graphiques superposant le modèle global aux quotients observés sur l'ensemble de âges de 0 à 100 ans.
Les âges élévés conduisant à des quotients supérieurs à 0,55 ont été tronqués puisque correspondant à des taux très élévés calculés sur des échantillons extrêmemnt réduits (0,50 correspond souvent à 2 ou 4 survivants dont 1 ou 2 décèdent). L'âge au décès du dernier mourant justifie, généralement, l'extrapolation qui est faite par le modèle.
| XVII-1 (1601 - 1650) | XVII-2 (1651 - 1700) |
 |
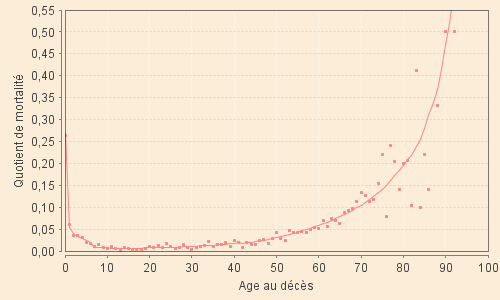 |
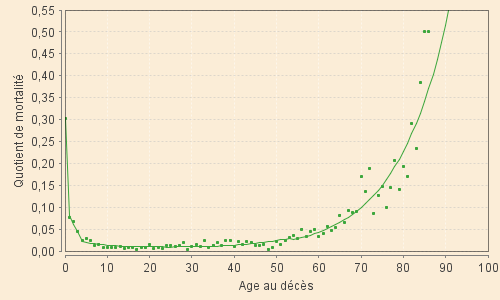
| XVIII-1 (1701 - 1750) | XVIII-2 (1751 - 1800) |
 |
 |
| XIX-1 (1801 - 1850) | XIX-2 (1851 - 1900) |
 |
 |
Ainsi, avec un modèle à 7 paramètres (2 coefficients pour chacun des segments de droite approximant la mortalité des « jeunes », l'âge de plafonnement de la mortalité de type « jeunes » et les 2 coefficients de la mortalité des « vieux »), l'objectif initial paraît être atteint (on doit éventuellement ajouter 4 paramètres, nombre pouvant être fortement réduit, d'ajustement aux âges élevés pour le XVIIe siècle) :
Nous gardons à l'esprit que, si le modèle s'accorde tant aux périodes récentes (XIXe siècle) qu'aux anciennes (XVIIe siècle), il n'est en toute rigueur défini qu'à Fontcouverte. Il est cependant probable qu'il peut-être utilisé dans bien d'autres communautés (rurales ?) de Maurienne, voire de France. Son emploi pour le XXe siècle est peut-être moins envisageable du fait de nouvelles conditions de vie (nouveaux modes de vie pour les 20 - 30 ans, report à des âges tardifs de la mortalité par vieillesse et apparition de centenaires modifiant les probabilités de décès à ces âges).