Une représentation théorique du développement d’une épidémie de peste

Les épidémiologistes et les mathématiciens actuels sont devenus experts dans l’étude quantitative des épidémies de nombreuses maladies, en particulier pour tenter de prévoir leur évolution quand elles se sont déclarées et déterminer les meilleurs moyens pour éviter leur développement et leur retour.

Nous essayons d’utiliser de façon très simpliste leurs méthodes pour étudier rétrospectivement l’épidémie de peste de 1630 en Maurienne en tentant de définir un modèle théorique censé représenter grossièrement une épidémie réelle.

Le principe de la méthode est de :

• déterminer les stades successifs de la maladie (infection, contagion... décès) depuis l’arrivée du premier infecté dans une communauté jusqu’à la mort ou la survie des derniers malades,
• définir les conditions qui font passer les victimes d’un stade de leur maladie au suivant et définir des lois supposées représenter quantitativement ces transferts.

Pour le cas particulier de la peste et comme on la connaît en Maurienne en 1630, on définit les stades suivants de la maladie dans une communauté.

• Les susceptibles S sont les personnes en bonne santé mais non immunisées naturellement contre la peste dans la mesure où la dernière épidémie remonte à 30 ans (naturellement il n’existe aucun vaccin à l’époque). Elles représentent, avant la première infection, la totalité de la population.
• Les infestés I sont les personnes qui viennent d’être contaminées quel que soit le mode de contamination. On admet qu’en début d’épidémie une personne de la communauté est dans ce cas et donc en mesure de débuter une contamination. Les infestés restent dans cet état pendant toute la période d’incubation de la maladie pendant laquelle, ils ne sont pas contagieux.
• Les contagieux C constituent le stade suivant pendant lequel les personnes infectées peuvent transmettre la maladie.
• Les morts M sont ceux qui ne résistent pas à la maladie.
• Les rétablis R sont ceux qui, au contraire, surmontent la maladie et ont acquis une immunité contre la peste au moins pour le temps pendant lequel l’épidémie persiste.

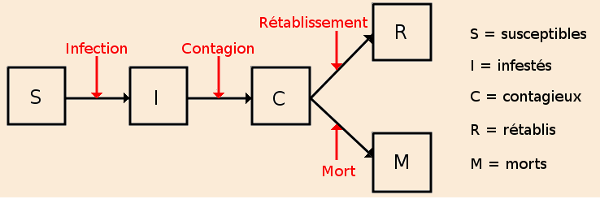
Les conditions retenues de passage d’un stade à l’autre sont les suivantes :

• De S à I. Un infectieux peut avoir, durant sa période d’infection, un nombre N de contacts directs ou par l’intermédiaire des puces avec ses voisins et infester, parmi ceux‑ci, ceux qui sont susceptibles. Le nombre de personnes que l’ensemble des infectieux contamine est proportionnel au nombre I des infectieux, au nombre S des susceptibles et au nombre N (N dépend de la contagiosité de la maladie et des facilités locales de contact).
• De I à C. Au terme d’une période d’incubation Ti de quelques jours, les infectieux deviennent contagieux en nombre proportionnellement à I et avec un taux journalier 1/Ti.
• De C à R. Au terme d’une période de contagion Tc de quelques jours, les contagieux peuvent, avec une certaine probabilité r se rétablir par guérison en nombre proportionnel à C et avec un taux journalier 1/Tc. Ils sont alors pourvus d’une immunité contre la maladie qu’ils viennent de surmonter. On admet que cette période d’immunité dure plus longtemps que celle de l’épidémie de peste (quelques mois).
• De C à M. Au terme d’une période de létalité Tl et avec une probabilité 1 – r intervient la mort concernant des individus en nombre proportionnel à C et avec un taux journalier 1/Tl.

On peut imaginer le fonctionnement du modèle en considérant des réservoirs d’eau se vidant les uns dans les autres, au cours du temps, suivant les lois régissant les transferts décrits ci‑dessus.

Le réservoir S comprend au départ l’ensemble de la population d’une communauté considéré comme indemne de maladie à l’exclusion cependant d’un individu infecté important le mal. La contagion se propageant dans le temps, des individus passent progressivement dans les réservoirs I, C, R ou M.

S, n’ayant que des sorties, voit son niveau baisser en permanence au cours de l’épidémie.

R et M, n’ayant pas de sortie, cumulent, au contraire, les individus de leur catégorie.

Les réservoirs I et C ont des niveaux variables à la montée ou à la baisse au cours du temps suivant que leurs entrées sont, à chaque instant, supérieures ou inférieures en nombre à leurs sorties.

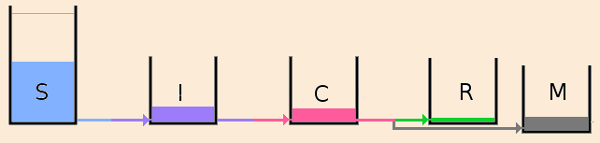
A tout instant S + I + C + R + M reste constant et égal au volume P de la population.

Le modèle est alors activé en découpant le temps de l’épidémie en instants courts par rapport à la durée de l’épidémie. Dans ce qui suit le pas de calcul est pris de 1 jour.

Au début des calculs S comporte P – 1 (ou plusieurs) personnes et I 1 (ou plusieurs) personnes, les autres états étant vides.

A chaque pas temporel successif, on calcule par les lois de transfert retenues le nombre d’individus passant d’un état à son suivant. On peut, au terme du calcul des jours successifs couvrant la période d’épidémie, tracer les courbes correspondant :

• aux nombres de présents dans les divers états (réservoirs),
• aux flux de personnes s'écoulant d’un état à son successeur.

Ainsi, à un instant donné, connaît on en particulier le nombre des personnes qui n’ont pas été infestées, celui des morts depuis le début de l’épidémie et celui des rétablis immunisés.

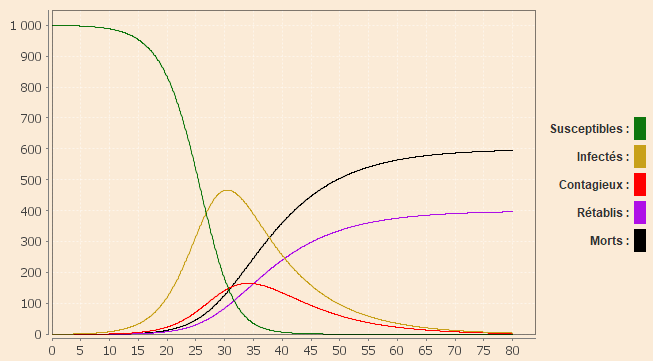
Le graphique ci‑contre est un exemple fictif d’épidémie très virulente atteignant une population de 1000 personnes mais dont une proportions importante des victimes survivent. Le temps, sur l'axe horizontal, est gradué en jours depuis le début d'épidémie. Les effectifs aux divers stades de la maladie sont exprimés, suivant l'axe vertical, en nombre d'individus. Les paramètres utilisés sont :
N = 2, Ti = 10 jours, Tc = 4 jours, Tl = 4 jours, r = 0,4.

Au terme de 80 jours d’épidémie :

• pratiquement toute la population a été contaminée,
• 600 individus sont morts,
• mais 400 ont survécu et ont été immunisés.

Le choix de N relativement élevé conduit donc à une contagion générale.

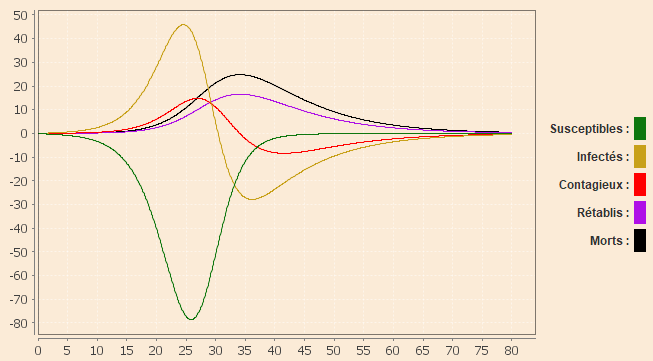
Les courbes des variations journalières des effectifs de chaque réservoir montrent un pic de mortalité journalière (courbe noire) à 35 jours atteignant 25 morts par jour. La courbe verte des susceptibles montre la baisse (d’où le signe moins) rapide des effectifs S dans la phase explosive de l’épidémie puis un ralentissement prononcé quand les susceptibles se raréfient.

L'histoire de l'épidémie comporte nettement 3 phases :

• une phase initiale où la maladie se met progressivement en place sous l'effet des durées de passage dans les états successifs,
• une phase d'explosion quand la contamination s'est répandue mais quand le nombre de personnes susceptibles est encore important,
• une phase terminale où le mal cesse par disparition des susceptibles et où ne se trouvent plus que les personnes immunisées.

Il est évident que ce calcul est plutôt caricatural mais il permet de se faire une idée de l’évolution d’une épidémie. En particulier la fixation des paramètres utilisés est arbitraire bien que voisins de ceux de la peste dans une agglomération à habitat resserré (valeur de N élevée).

On imagine aisément qu’un modèle sérieux de peste devrait au moins être triple et comprendre :

• un sous modèle de l’évolution de l’épidémie chez les rongeurs,
• un sous modèle de celle des puces,
• un sous modèle de l’épidémie humaine.

Chaque sous modèle, avec ses propres paramètres, interférerait avec les autres. On pourrait alors aborder le problème de la fin de l’épidémie en tenant compte du comportement spécifique des rats et surtout des puces en fonctions des variations climatiques ce qui conduirait à l’arrêt de l’épidémie alors que des susceptibles resteraient en nombre. Mais les informations nécessaires sont pour nous hors de portée : pleuvait il ou faisait il sec le 20 novembre 1630 à Modane ou faisait il déjà froid pour faire disparaître les puces ?

Nous ne nous servons du modèle (nous avons retenu la fonction de HUBBERT) que pour définir la forme de l’explosion initiale de l’épidémie (courbe des morts) et estimer les reprises successives de l'épidémie.

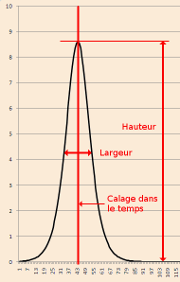
On peut alors retenir comme bonne approximation la courbe de mortalité ci‑contre pour représenter une éruption isolée de contagion pesteuse.

Ce modèle comporte 3 paramètres à ajuster aux décès observés :

• la hauteur de l’éruption soit le nombre de morts journaliers maximum,
• la largeur à mi hauteur de l’éruption qui traduit son étalement dans le temps,
• le calage du pic de l’éruption dans le temps.

La surface sous la courbe traduit le nombre total de décès qu’on peut attribuer à l’éruption.

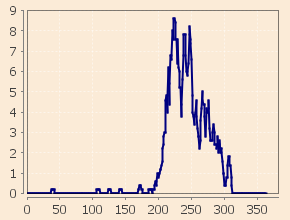
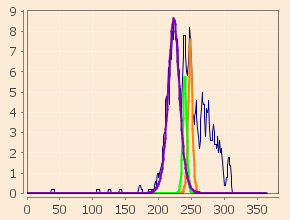
Relatives à l’épidémie observée à Modane en 1630, les figures suivantes donnent avec sur l'axe horizontal les jours comptés depuis le 1^er janvier 1630 et sur l'axe vertical le nombre de morts journalier :

• à gauche, le nombre journalier de morts donné par les archives (en moyenne mobile sur 5 jours),
• au centre, la superposition des 3 pics initiaux calculés dont le premier particulièrement importants de début d'épidémie,
• à droite, la somme temporelle des 3 pics s'ajustant bien à la courbe des décès observés en phase initiale.

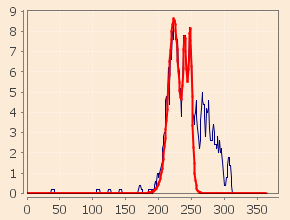Il apparaît naturellement que nos calculs ne sont que des approximations. Le premier pic, par exemple, ne correspond pas exactement à un pic isolé. En effet, il est lui‑même la superposition de plusieurs éruptions mineures relativement jointives dans le temps. Il faudrait connaitre exactement la localisation de chaque décès à Modane pour interpréter de tels détails et avoir ainsi un aperçu de la propagation de la peste dans la ville, ses quartiers, ses maisons.