Le filtre de la moyenne mobile

De nombreux phénomènes étudiés à Fontcouverte, par exemple le nombre annuel des naissances au cours du temps, manifestent une grande variabilité interannuelle liée au phénomène lui-même qui superpose :

• des fluctuations très rapides dans le temps apparaissant comme aléatoires dans la mesure où on ne les explique pas ; qui peut prédire combien de naissances arriveront telle année bien que tout soit presque prévisible de nombreux mois à l'avance ?
• des évolutions plus progressives dans le temps liées à la variation de la natalité suivant le volume de la population ou la succession de périodes favorables ou désastreuses, évolutions qui sont ce qui nous intéresse dans notre étude.

Le graphique ci-dessous présente le nombre annuel des naissances (trait fin) fortement fluctuant et le résultat d'une transformation (trait gras) décrite ci-dessous qui permet de « lisser » les fluctuations rapides de façon à mieux laisser apparaitre les évolution à long terme.

Moyenne mobile de valeurs simples

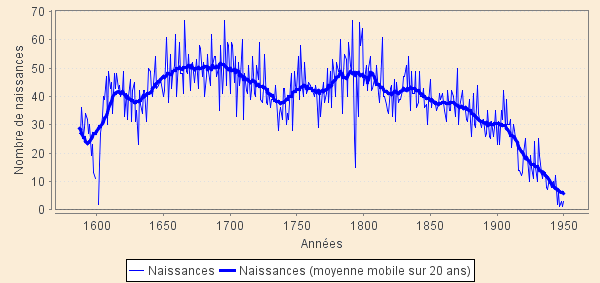
Pour réaliser ce lissage, on pourrait calculer le nombre de naissances par décennies puisque l'on sait que la moyenne de 10 nombres aléatoires est moins dispersée que ces nombres (par exemple, les fluctuations annuelles sont 3 fois plus importantes que leur moyenne sur 10 ans et 4 à 5 fois plus que leur moyenne sur 20 ans). Mais on n'aurait plus que 10 ou 5 points par siècle qu'on ne saurait trop comment joindre.

On peut aussi calculer la moyenne décennale des 10 valeurs centrées sur une année donnée puis faire le même calcul pour les années suivantes (ou précédentes). Il s'agit alors d'une « moyenne mobile » qui glisse sur les années. On filtre ainsi les variations rapides du phénomène étudié : plus l'intervalle de temps servant au calcul de la moyenne est grand, plus ne restent apparentes que les tendances à long terme, terme croissant avec la durée de l'intervalle de temps utilisé.

Tout l'emploi de la moyenne mobile repose alors sur un choix judicieux de l'intervalle de calcul, adapté aux phénomènes que l'on veut faire disparaitre (considérés comme aléatoires) et à ceux que l'on veut mettre en évidence (considérés comme significatifs).

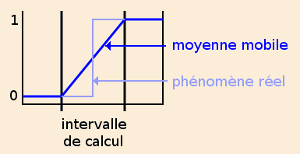
Ce procédé de calcul n'est pas sans défaut si l'on s'intéresse à une variation brusque de la tendance à long terme. Par exemple, si l'on traite un phénomène passant brutalement d'une valeur 0 à une valeur 1, l'échelon qu'il présente sera transformé en une rampe fictive sur l'intervalle qui a servi au calcul de la moyenne mobile. Il importe alors de réduire cet intervalle, au risque d'augmenter la dispersion, pour mieux définir la date exacte de l'échelon.

Dans notre étude de Fontcouverte, de nombreux graphiques présentés avec une moyenne mobile sont réalisés avec l'intervalle qui nous parait le meilleur pour illustrer les variations qui nous intéressent. Cependant, il a toujours été étudié des intervalles plus grands ou plus faibles, éventuellement plus difficiles à interpréter, de façon à contrôler les conclusions tirées.

Moyenne mobile de quotients

Les lecteurs qui n'apprécient pas les calculs peuvent s'arrêter ici et simplement nous croire dans nos présentations puisque nous abordons maintenant des cas moins fréquents.

Un calcul particulier est à envisager si la moyenne mobile porte sur un quotient tel qu'un pourcentage de personnes présentant une caractéristique particulière dans une population comme, par exemple, le quotient C = A / B du nombre A des célibataires rapporté au volume B de la population, quotient qui serait observé à deux instants, soit à titre d'illustration très simple :

La moyenne ordinaire C* des quotients est (C₁ + C₂) / 2 = 0,300.

Le quotient moyen réel C sur l'ensemble des deux instants est C = (A₁ + A₂) / (B₁ + B₂) = 0,167.

L'écart est ici important et provient des ordres de grandeur très différents de B₁ et B₂. En effet, des expressions précédentes on déduit : A₁ = C₁ * B₁ et A₂ = C₂ * B₂. Ainsi C = (C₁ * B₁ + C₂ * B₂) / (B₁ + B₂) est simplement une moyenne de C₁ et C₂ pondérés par les valeurs respectives B₁ et B₂.

Si l'on ne connaît que C₁ et C₂ (comme ce serait le cas si ces valeurs provenaient de résultats bibliographiques sans autres précisions) il est évident que ces calculs sont impossibles. Heureusement pour nous, ces valeurs sont, dans notre étude, le résultat de calculs du type C = A / B une fois déterminées les valeurs A₁, A₂, B₁ et B₂. Nous pouvons donc calculer directement la moyenne mobile C de N valeurs en partant de celles des A et des B que nous connaissons.

Nous appliquons cette méthode toutes les fois qu’une moyenne mobile se rapporte à un rapport (quotient, probabilité, pourcentage…)